Physics in Action (Animation in Java without GUI)

This is the mirror of the closed site at:

http://www.blueneptune.com/~xmwang/physDemo.html

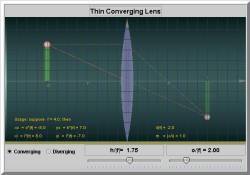Interactive Physics	3D Modern Physics I: Rotation	Physics in Virtual Reality	Physics Simulations using Swing/Java2D

Non-interactive Physics Demo

Contents

• Thermophysics
• Two Coordinate Oscillation
• Magnus Force
• Sound of Music
• Three-Phase AC Circuits
• Enginerring Mechanics
• Optics (new, using Swing/Java2D)
• Science, Engineering and Art

  

  ---

  ThermoPhysics

  • Animation: Carnot Engine and Carnot Cycle
  • Animation: Otto Engine and Otto Cycle
  • Animation: Diesel Engine and Diesel Cycle

  ---

  The Two-Coordinate Harmonic Oscillation

  Brief Discussion

  The Equations (ODE2):

  d^2 x1/dt^2 = - k1*x1 - k2*(x1 - x2) - 9.8*fk*dx1/dt; d^2 x2/dt^2 = - k1*x2 - k2*(x2 - x1) - 9.8*fk*dx2/dt;

  The Initial Conditions:

  x1 = x1(0); x2 = x2(0); v1 = 0; v2 = 0;

  Mass and Coefficients Convensions:

  We have set m1 = m2 = 1 (dimensionless). This means we have also set: our k1 = k1/m and our k2 = k2/m, where m is the mass of each cart

  Reference:

  Grant R. Fowles and George L. Cassiday: Analytical Mechanics, 5th Edition, Saunders College Publishing, section 11.3, pp. 382.

  • First, assuming there is no friction. We have typically three different initial conditions: swapping, same-phase and opposite phase.
    • Animation: a system of two-cart + three-spring swapping without friction
    • Simulation: Displacements of Two-Carts in Swapping Oscillation
    • Animation: x1(0) = -x2(0) = 1 , opposite phase without friction
    • Simulation: Displacements od Two Carts in Opposite Phase Oscillation, no friction
    • Animation: x1(0) = x2(0) = 1 same phase without friction

  • But friction dos exist. We assume it only depends on the direction of motion(constant in mafnitude), and when v = 0, fricrion = 0. We can see damped oscillation (but not exponentially damped).
    • Animation: a system of two-cart + three-spring swapping with friction
    • Simulation: Displacements of Two-carts in Swapping Oscillation, with friction
    • Animation: x1(0) = -x2(0) = 1 , opposite phase with friction
    • Simulation: Displacements of Opposite Phase Oscillation, with friction
    • Animation: x1(0) = x2(0) = 1 same phase with friction

  

  ---

  The Magnus Force

  • Animation: K = 0.11, angle=π/6 with v0 = 8m/s, Tou = 2.0 sec
  • Animation: K = 0.12, angle=π/6 with v0 = 8m/s, Tou = 2.5 sec
  • Animation: K = 0.12, angle=π/3 with v0 = 6m/s, Tou = 2.0 sec
  • Animation: K = 0.18, angle=π/6 with v0 = 6m/s Tou = 3.0 sec

  After we have found the best fitting K and Tau, then we can simulate some Magnus motion which is very hard to do in a real Lab. Here we let K = 0.12, Tou = 2.5 sec, Q0 = π/4, and let v0 = 30m/s and 45 m/s respectively. The animations are:

  • Animation: K = 0.12, v0 = 30m/s
  • Animation: K = 0.12, v0 = 45m/s

  

  ---

  The Sound of Music

  • Graph: standing waves
  • Simulation: vibrating string (zeroth mode)
  • Simulation: vibrating string (first mode)
  • Simulation: vibrating string (linear combination of three modes)
  • Graph: string length vs. frequency.

  Traveling Wave and Vibtation Along a String

  • Simulation: a traveling wave, zeroth mode .
  • Does wave really travel? zeroth mode .

  • Simulation: a traveling wave, first mode .
  • Does wave really travel? first mode .

  • Simulation: a traveling wave, linear combination of first three modes .
  • Does wave really travel? combination of first three modes .
  • the wave equation

  

  ---

  Three-Phase AC Currents

  • Simulation:3-Ph AC generator/Motor
  • simulation: three rotating Current vectors

  

  ---

  Engineering Mechanics

  • Enginerring Statics

    • Simulation: A Uniform Cable and Catenary Curve
    • Animation: A Uniform Cable with Changing Sag

  • Fluid Dynamics
    • Some exact solutions of the Navioer-Stokes Equations
      • simulation: The Flow Near an Oscillating Flat Plate
      • simulation: Two Solitary Waves on the Water-Surface in a Canal
      • simulation: 1D diffusion Equation
        • dF/dt = alpha* d^2 F/dx^2;
        • alpha=0.00001; F(x,0) =0; F(0,t) = F(1,t) = 100.

      • Potential Flow: Potential flow near a cylinder at rest

      • Magnus Flow: Magnus flow near a spinning cylinder

    • Galerkin's Final Element Method:
      • 1-D Roof Functions

      • Flow Through Parallel Plates

    ---

    Science, Engineering and Arts

    • Science and art

    ---

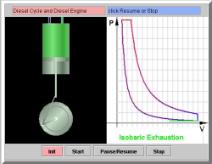
    Physics Simulations Using JApplet/Swing/Java2D

    ---

    
    

    ---