Two Carts

Coupled Harmonic Oscillation

By Dr. Xing Min Wang

If you do not see the Applet, please install Java Plug-in 1.4.0

The Equations (ODE2):

d^2 x1/dt^2 = - k1*x1 - k2*(x1 - x2) - 9.8*fk*dx1/dt;
d^2 x2/dt^2 = - k1*x2 - k2*(x2 - x1) - 9.8*fk*dx2/dt;

The Initial Conditions:

x1 = x1(0); x2 = x2(0); v1 = 0; v2 = 0;

Mass and Coefficients Convensions:

We have set m1 = m2 = 1 (dimensionless).
This means we have also set:
our k1 = k1/m and our k2 = k2/m,
where m is the mass of each cart

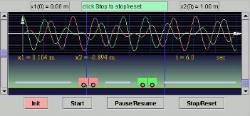
Displacement vs. Time:
Pink curve is corresponding to the motion of the pink cart.
Green curve is corresponding to the motion the green cart.

Typical cases:

Two-Carts in Swapping Oscillation, no friction
Parameter set: x1(0) =0.0,x2(0) = 1.0, k1 = 81.0, k2 = 20.0, fk = 0.0
Two Carts in Opposite Phase Oscillation, no friction Parameter set: x1(0) =1.0,x2(0) = -1.0, k1 = 81.0, k2 = 20.0, fk = 0.0
Two-carts in Swapping Oscillation, with friction Parameter set: x1(0) =0.0,x2(0) = 1.0, k1 = 81.0, k2 = 20.0, fk = 0.2
Two-carts in Opposite Phase Oscillation, with friction Parameter set: x1(0) =-1.0,x2(0) = 1.0, k1 = 81.0, k2 = 20.0, fk = 0.2

Reference:

Grant R. Fowles and George L. Cassiday:
Analytical Mechanics,
5th Edition, Saunders College Publishing, section 11.3, pp. 382.